Conceptos básicos de estadística

Existen ciertos conceptos que necesitamos conocer para poder iniciarnos en la estadística. Aquí describo algunos de ellos:

Definiciones básicas

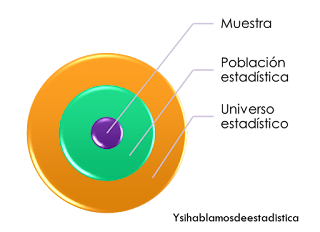
Universo estadístico

Es el conjunto, finito o infinito, de elementos sobre los cuales están definidas las características que se van a analizar. Note que, el universo estadístico corresponde a lo que comúnmente llamamos población.

Población estadística

Es el conjunto de mediciones u observaciones de cada una de las características que se desean analizar, es decir, la población estadística estará formada por los valores de las variables del estudio.

Censo

Es el estudio de todos y cada uno de los elementos del universo estadístico.

Muestra

Cuando no es posible realizar un censo, debido a costos, tiempo, etc. es recomendable utilizar una muestra. Esta comprende una porción de la población y es encontrada mediante métodos de muestreo.

Variable

Característica que se desea estudiar. El valor de una variable para un elemento del universo estadístico se conoce como dato. Existen distintos tipos de datos, lo que conlleva a tener distintos tipos de variables, como lo son las variables cualitativas y variables cuantitativas:

• Variables cualitativas: aquellas que representan cualidades, en otras palabras, son datos correspondientes a atributos que conforman categorías.
• Variables cuantitativas: aquellas que representan cantidades. Pueden ser discretas, como número de años cumplidos o número de hermanos, en las que no es posible encontrar un valor entre dos valores consecutivos de ella (correspondiéndose al conjunto de número Naturales). O también pueden ser continuas, en donde si es posible encontrar un valor entre dos valores consecutivos por más cercanos que se encuentren, como la estatura o el peso.

Escalas de medida
Existen distintos tipos de datos, por tanto, son medidos de manera diferente de acuerdo a las escalas de medida:

• Escala nominal: conformada por datos que representan atributos en donde solo se pueden establecer relaciones de igualdad o diferencia, como en la variable sexo o estado civil. Además, las categorías o atributos de una variable de escala nominal son mutuamente excluyentes, es decir, un individuo puede clasificarse en solo una de las categorías de la variable.
• Escala ordinal: atributos en donde además de las relaciones de igualdad es posible jerarquizar, como en el grado de instrucción o grado militar.
• Escala absoluta: está constituida por todos los números entero positivos y el cero, por ejemplo, número de zapaterías en una ciudad o número de habitantes en un país.
• Escala proporcional o de razón: conformada por el conjunto de números Reales, por tanto, es posible realizar operaciones algebraicas y establecer relaciones de igualdad o diferencia. Como por ejemplo el nivel de hemoglobina, tiempo empleado en realizar un trabajo o ingreso familiar.
• Escala de intervalos:la constituyen números en donde solo es posible establecer relaciones de igualdad o diferencia y también distancias; además poseen un cero relativo que no indica ausencia de la característica, como por ejemplo la temperatura en grados centígrados o altura sobre el nivel del mar. Se utilizan también en el análisis de mercado cuando se quiere conocer  el nivel de acuerdo o desacuerdo en determinadas afirmaciones (1= totalmente en desacuerdo, 3= ni de acuerdo ni es desacuerdo, 5= totalmente de acuerdo). 

Según lo anterior, cada tipo de variable es medida de acuerdo a una escala, en efecto:

Ramas del análisis estadístico

Estadística descriptiva

Proceso en el que se resumen y describen conjuntos de datos, de manera que sus características sean fáciles de visualizar.

Estadística inferencial
Proceso que utiliza una muestra para sacar conclusiones sobre una población. Estas conclusiones son hechas a partir del cálculo de estadísticos, que a su vez estiman los parámetros.

Parámetro: Medida que describe la población o el total de las observaciones de interés.
Estadístico: Medida que describe una muestra y que además sirve para estimar el parámetro de la población.
Error de muestreo: Diferencia entre el estadístico y el valor real y desconocido del parámetro. Esto ocurre cuando la muestra no es representativa de la población.

Veamos un par de ejemplos (tomados de Armas, J. (1998)):

Ejemplo 1. Una empresa piensa instalar una clínica en una ciudad y dentro del estudio de factibilidad se requiere conocer el nivel de ingreso familiar mensual de la ciudad.

• Variable: Ingreso familiar mensual.
• Tipo de variable: cuantitativa continua y escala proporcional.
• Universo: Todas las familias o núcleos familiares de esa ciudad.
• Población: El ingreso familiar de todas las familias de la ciudad.
• Muestra: Los ingresos familiares de 30 familias de esas ciudad.
• Parámetro: Ingreso promedio de todas las familias de la ciudad.
• Estadístico: Ingreso promedio de 30 familias de esa ciudad.

Ejemplo 2. Una droguería pretende lanzar al mercado un nuevo medicamento contra el dolor de cabeza y requiere conocer la efectividad de la misma.

• Variable: Efectividad del medicamento.
• Tipo de variable: Para establecer el tipo de variable debemos tener en cuenta cómo la vamos a medir, pudiendo ser:
• Cualitativa con escala nominal: ¿Me quitó el dolor? 
• Si
• No
• Cualitativa con escala ordinal: ¿Qué tan efectivo fue el medicamento? 
• Muy efectivo (me quito el dolor).
• Regular (la intensidad del dolor bajó pero no me lo quitó).
• No fue efectivo (el dolor no cesó).
• Cuantitativa discreta o con escala absoluta: Desde que tomé el medicamento, ¿cuántas horas pasaron para que hiciera efecto?
• De 1 a 2 horas
• 2 a 3 horas
• 3 horas o más
• Cuantitativa continua con escala proporcional: Desde que tomé el medicamento, ¿cuánto tiempo pasó para que hiciera efecto?, pudiendo ser horas y minutos, hora y media por ejemplo.
• Universo: Todas las personas con dolor de cabeza en un momento determinado y las que potencialmente puedan tener dolor de cabeza en el futuro.
• Población: Las reacciones de las personas luego de tomar el medicamento.
• Muestra: Las reacciones ante el medicamento de un grupo de 20 personas.

Referencias

Armas, J. (1988). Estadística Sencilla Descriptiva. Venezuela: Universidad de Los Andes.

Webster, A. (2000). Estadística aplicada a los negocios y la economía. Tercera Edición. McGraw-Hill.
Aldás y Uriel (2017). Análisis multivariante aplicado con R. Segunda Edición. Paraninfo, S.A.