Teoría de Conjuntos

Para estudiar probabilidades debemos tener en cuenta una serie de definiciones acerca de la teoría de conjuntos. Pero, ¿qué es la teoría de conjuntos?.

La teoría de conjuntos es una rama de la matemática que estudia las características, propiedades y relaciones en una colección de objetos.

Definiciones

Conjunto

Colección de objetos o elementos con alguna característica en común. Usualmente se denotan con las primeras letras del alfabeto en mayúsculas y pueden definirse por extensión o por comprensión.

- Extensión: Al definir un conjunto por extensión, se escriben todos y cada uno de los elementos que forman parte del conjunto. Ejemplo: A = {2,4,6,8}

- Comprensión: Al definir un conjunto por comprensión, se escribe una característica que identifique a todos los elementos del conjunto. Ejemplo:

A = { x | x es un número par mayor que 0 y menor que 10}

A = { x | 0 < x < 10}

Subconjunto

Conjunto cuyos elementos están contenidos en otro. Se denota como A ⊂ B y se lee A está contenido en B.

Conjuntos Equivalentes

Si A ⊂ B y B ⊂ A entonces A = B.

Conjunto Vacío

Conjunto que no tiene elementos. Se denota por ∅.

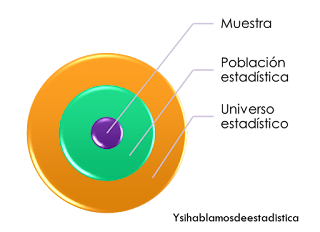
Conjunto Universo

Conjunto que contiene todos los elementos de una determinada situación y se denota por Ω. Ejemplo: A y B son subconjuntos de Ω.

Álgebra de conjuntos

Unión La unión de A y B, denotada por A ∪ B, es el conjunto formado por los elementos que están en A o en B o en ambos.

Intersección La intersección de A y B, denotada por A ∩ B, es el conjunto formado por los elementos que están en A y B a la vez.

Complemento Sea A ∈ Ω, el complemento de A es el conjunto de todos los elementos que están Ω pero no en A. Se denota como A'.

Diferencia La diferencia de A y B, denotada por A - B, es el conjunto formado por los elementos que están en A pero no en B.

Conjuntos disjuntos o mutuamente excluyentes Se dice que A y B son disjuntos o mutuamente excluyentes si A ∩ B = ∅, es decir, la intersección de estos conjuntos es vacía, la ocurrencia de uno implica la no ocurrencia del otro.

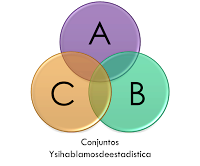
Diagramas de Venn

Representación gráfica de las relaciones que pueden haber en los elementos de uno o varios conjuntos. Si se grafican las interacciones explicadas anteriormente, se tiene:

Algunas propiedades

El álgebra de conjuntos nos permite establecer algunas propiedades:

Referencias

Mood, Graybill & Boes (1974). Introduction to the theory of statistics. Tercera Edición. McGraw-Hill .